Introduction

This post continues the series of posts describing experiments with using an FPGA as a high-speed (millions of samples per second) data capturing device. It continues from my previous post, where we defined the exchange protocol and measured timing. As I concluded in that post, we need to have a buffer on the capturing device side, which can hold the samples if the computer temporarily stops polling the data due to handling OS interrupts.

Conveniently, FPGAs typically have RAM on the chip, which can be used for building such a buffer, and we will explore how to use it in this post. We will create a simple data generator that will simulate the data and write it into the buffer, and then read the data from the buffer and transfer it to the parallel bus.

This test program partially implements my project of building a microphone array with multiple INMP441 microphones connected to the FPGA, which I will briefly describe in the next section.

High level design overview

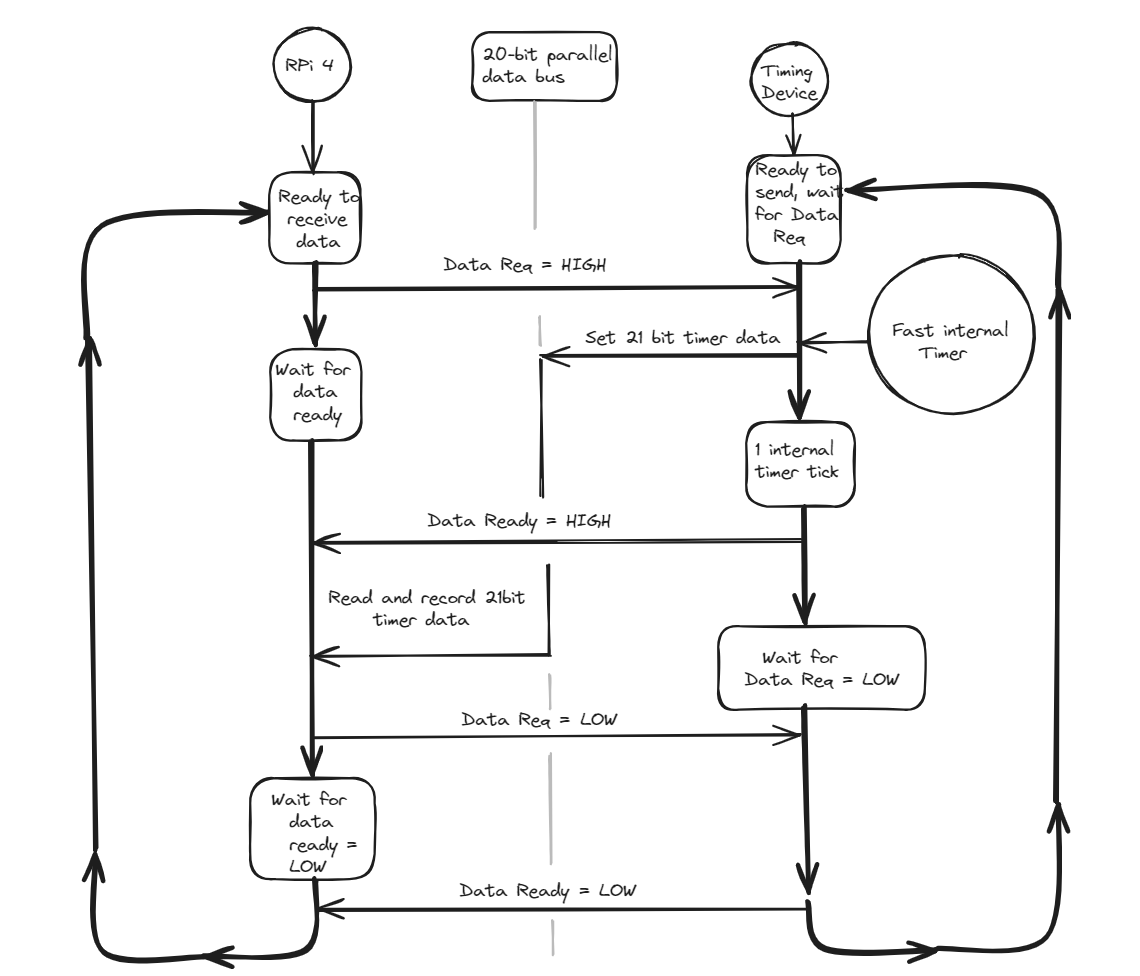
Here is the diagram of the digital device I am having in mind

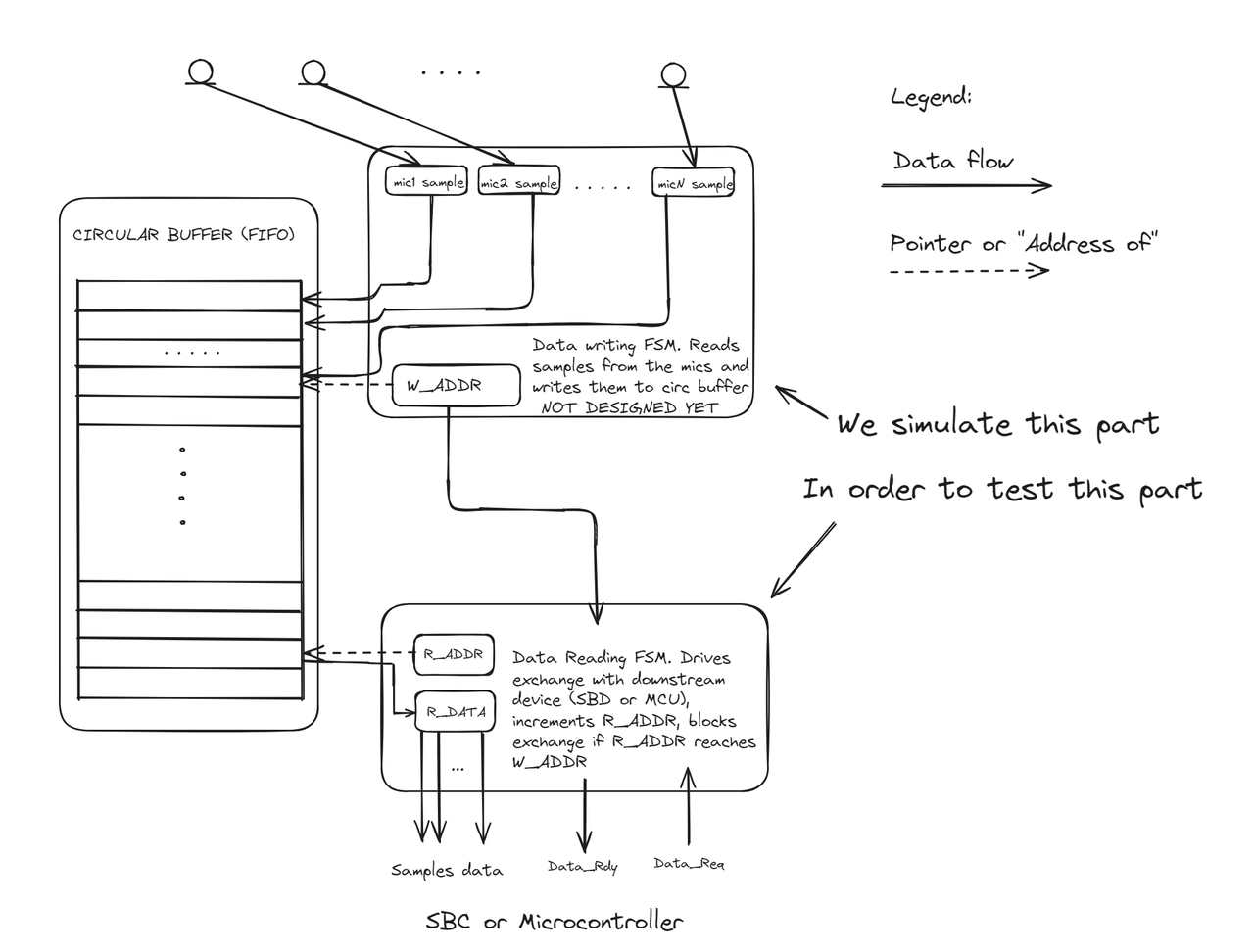
According to our estimation, we need a buffer of size > 260 samples. We will implement a 512-sample buffer, which will have extra space to cover cases when two interrupts come almost simultaneously.

The iCE40HX1K chip has 16 blocks of RAM, each with 4096 bits (512 bytes). Each block can be configured for storing 256 x 16-bit, 512 x 8-bit bytes, 1024 x 4-bit, or 2048 x 2-bit memory cells. Since I am aiming to capture 24-bit samples from multiple INMP441 microphones, my samples are 24-bit wide. To utilize the memory efficiently, I decided to use 3 blocks configured as 512x8: the 1st block will keep bits 0-7, the 2nd block will keep bits 8-15, and the 3rd block will keep bits 16-23.

We will design the multiple I2S capturing part in the next posts. Today, we will replace it with simulated data, which will be written into the circular buffer, and focus on data reading and transferring to the parallel bus.

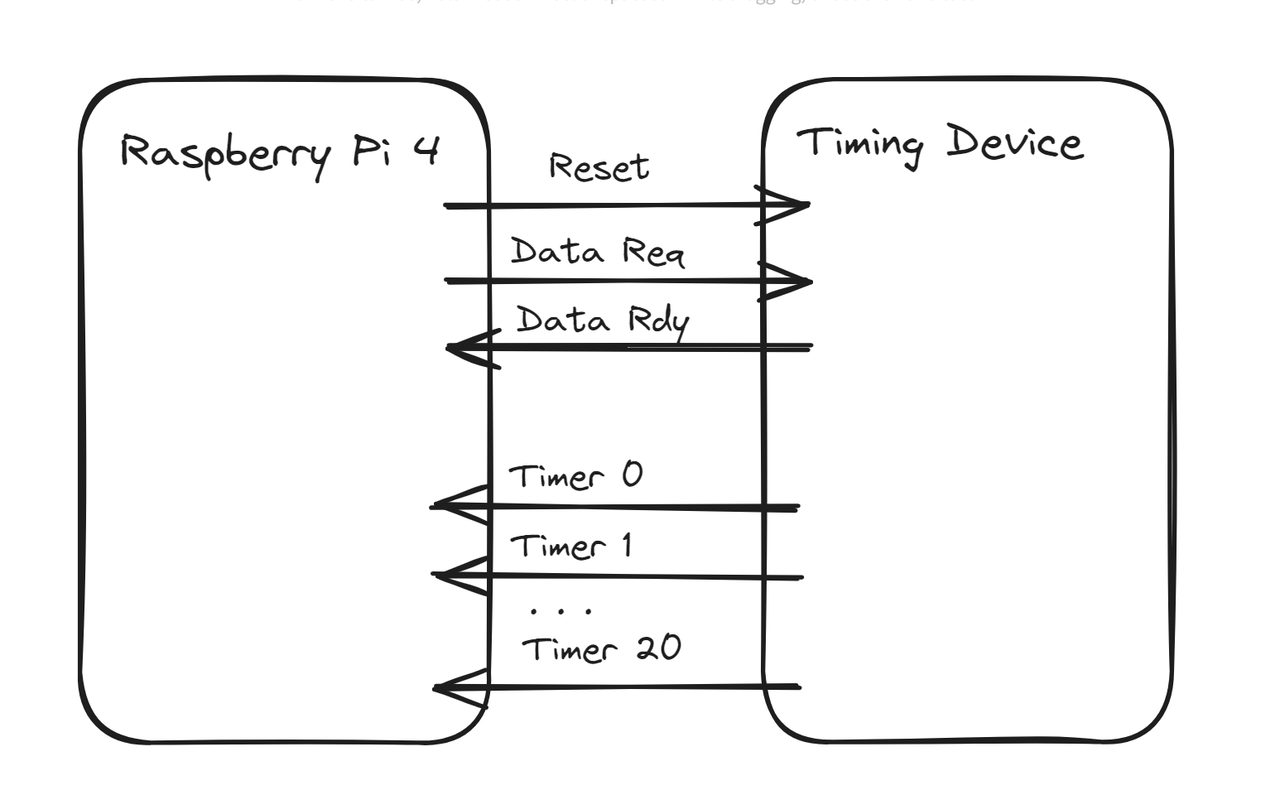
The exchange protocol is the same as in the time measurement setup described in the previous post: the "device" (FPGA) waits for the rising edge of the "Data Req" (data request) line and sets its 21-bit data output, but this time it reads it from the memory instead of using a timer value. Then the "device" sets the "Data Rdy" (data ready) line to HIGH. The polling program detects the change in the "Data Rdy" line, reads and records the 21-bit data value from the parallel bus, and then sets "Data Req" to low on the SBC. This signals to the device that the SBC has successfully read the data, prompting it to set "Data Rdy" to low. The polling program detects the falling edge of the "Data Rdy" line and proceeds to the next cycle iteration.

Previously, we used the timer value as the data. It is pretty much the same in this design, but the timer value is written to the FIFO buffer, and the reading part of the system gets it from the reading side of the FIFO and sends it to the parallel bus.

The timer is now 8-bit wide. We repeat it 3 times to get a 24-bit value, so the data should be the least significant 21 bytes of the 24-bit value {Timer[7:0], Timer[7:0], Timer[7:0]}. As a quick reminder, we are using a 21-bit data value because we ran out of pins on the iCEstick board.

Verilog implementation

I think there are modules similar to PLL (see the previous post) which can be used for defining the RAM block in Verilog. The Memory Usage Guide for iCE40 Devices mentions the SB_RAM512x8, SB_RAM1024x4 modules, but I think they are Lattice/iCE40-specific and I am not sure how to use them with apio.

There is also another, more portable way to infer RAM blocks in Verilog, which is supported by most of the FPGA synthesis tools. We will follow this way in our design. The following code snippet shows how to define a 512x8 memory block in Verilog which can be inferred as a Block RAM by the synthesis tool.

module ram512x8
(
    input [8:0] RADDR,
    input RCLK,
    input RE,
    output reg [7:0] RDATA,
    input [7:0] WDATA,
    input [8:0] WADDR,
    input WCLK,
    input WE
);
    reg [7:0] memory [0:511];

    integer i;

    initial begin
        for(i = 0; i < 512; i++)// start with blank memory with 0 instead of x so that we can infer Yosys for BRAM.
            memory[i] <= 8'd0;
    end

    always @(posedge RCLK)
    begin
        if (RE)
        begin
            RDATA <= memory[RADDR];
        end
    end

    always @(posedge WCLK)
    begin
        if (WE)
        begin
            memory[WADDR] <= WDATA;
        end
    end
endmodule

When the synthesis tool sees an array of registers with a specific read and write access pattern, which matches the RAM block (like one above), it will infer the RAM block instead of using the LUTs.

Here is how we define the buffer in our top-level module:

//Define memory access signals
wire [8:0] r_addr;
wire r_en;
wire [23:0] memory_read_value;
reg [8:0] w_addr;
reg [7:0] w_data;
reg w_en;


//We will use 3 blocks of 512x8 RAM to store 24-bit samples
//Each the blocks share read address (r_addr), write address (w_addr),
//write enable (w_en) and read enable (r_en) signals. We write the same
//value to all 3 blocks, (since it is simulated data), and read the data into
//different bits of the memory_read_value signal.

ram512x8 ram512X8_inst_0 (
    .RDATA(memory_read_value[7:0]),
    .RADDR(r_addr),
    .RCLK(ref_clk),

    .RE(r_en),
    .WADDR(w_addr),
    .WCLK(ref_clk),

    .WDATA(w_data),
    .WE(w_en)
);

ram512x8 ram512X8_inst_1 (
    .RDATA(memory_read_value[15:8]),
    .RADDR(r_addr),
    .RCLK(ref_clk),

    .RE(r_en),
    .WADDR(w_addr),
    .WCLK(ref_clk),

    .WDATA(w_data),
    .WE(w_en)
);

ram512x8 ram512X8_inst_2 (
    .RDATA(memory_read_value[23:16]),
    .RADDR(r_addr),
    .RCLK(ref_clk),

    .RE(r_en),
    .WADDR(w_addr),
    .WCLK(ref_clk),

    .WDATA(w_data),
    .WE(w_en)
);

The simulation part is pretty simple, we generate the data and write it into each buffer:

reg [4:0] counter;  //Controls stage of writing data into the buffer
reg [7:0] counter2; //Counter representing the simulated data

always @(posedge ref_clk) begin
    if (rst) begin
        w_addr <= 9'b0;
        counter <= 0;
        counter2 <= 0;
        w_en <= 0;
    end
    else begin
        if (counter == 3) begin
            counter <= 0;
            w_data <= ~counter2;
        end else if (counter == 4) begin
            w_en <= 1;
        end else if (counter == 5) begin
            w_en <= 0;
        end else if (counter == 6) begin
            counter2 <= counter2 + 1;
            w_addr <= w_addr + 1;
        end

        counter <= counter + 1;
    end
end

The average reading speed should be faster then writing speed. If the reader is interrupted for a brief period of time, the data will be buffered in the RAM. When the reader returns to polling the data, it will catch up with the writer. If the reader reaches the writer address, it will stop reading the data until the new data arrives.

I implemented the reader in a separate model since want to reuse it in different designs. Here is the verilog code for the reading part:

module parallel_exchange_fsm
(
    input rst,                  //Reset
    input clk,                  //12 MHz iCEstick clock
    input [8:0] w_addr,         //Current writing position so we know how much data is available

    //Interraction with memory
    output reg [8:0] r_addr,    //Reading address in buffer
    output reg r_en,            //Read enable
    input [23:0] memory_read_value, //

    //Interraction with downstream device
    input data_req,             //Data request signal
    output reg [23:0] data_out, //Output data
    output reg data_ready       //Data ready signal
);

    //Data request synchronization flip-flops
    reg data_req_1;
    reg data_req_2;

    localparam WAITING_DATA_REQ_HIGH = 2'b00;
    localparam WAITING_DATA_AWAIL = 2'b01;
    localparam READING_BUFFER = 2'b10;
    localparam WAITING_DATA_REQ_LOW = 2'b11;

    reg [1:0] paralled_data_io_state;

    //This FSM handles parallel data output
    always @ (posedge clk) begin
        if (rst == 1'b1) begin
            r_addr <= 9'b0;
            data_out <= 24'b0;
            data_ready <= 1'b0;
            data_req_1 <= 1'b0;
            data_req_2 <= 1'b0;
        paralled_data_io_state <= 2'b0;
        end else begin

            case (paralled_data_io_state)
                WAITING_DATA_REQ_HIGH: begin
                    r_en <= 1'b1;  //Just keep r_en high all the time for simplicity
                    if (data_req_1 & ~data_req_2) begin
                        paralled_data_io_state <= WAITING_DATA_AWAIL;
                    end
                end

                WAITING_DATA_AWAIL: begin
                    if (w_addr != r_addr) begin //Data available in the buffer
                        paralled_data_io_state <= READING_BUFFER;
                    end
                end

                READING_BUFFER: begin
                    r_addr <= r_addr + 1;
                    data_ready <= 1'b1;
                    data_out <= memory_read_value;
                    paralled_data_io_state <= WAITING_DATA_REQ_LOW;
                end

                WAITING_DATA_REQ_LOW: begin
                    if (~data_req_1) begin
                        paralled_data_io_state <= WAITING_DATA_REQ_HIGH;
                        data_ready <= 1'b0;
                    end
                end

            endcase

            data_req_1 <= data_req;
            data_req_2 <= data_req_1;
        end
    end

endmodule

Note that if there is no data in the buffer, r_addr == w_addr, the reader will stick in the WAITING_DATA_AWAIL state until the new data arrives. This is how we use it in the top-level module:

parallel_exchange_fsm parallel_exchange_fsm_inst
(
    .rst(rst),                  //Reset
    .clk(ref_clk),                  //12 MHz iCEstick clock
    .w_addr,         //Current writing position so we know how much data is available

//Interaction with memory
    .r_addr(r_addr),    //Reading address in buffer
    .r_en(r_en),            //Read enable
    .memory_read_value(memory_read_value), //

//Interaction with downstream device
    .data_req(data_req),             //Data request signal
    .data_out(data_out), //Output data
    .data_ready(data_rdy)       //Data ready signal
);

Tests and results

First of all we need to double check that the synthesis tool could infer the RAM blocks. We can do this by looking at the synthesis report generated by apio build command in "verbose" mode.

apio build --verbose

....Skipping some (a lot of) output...

Info: Device utilisation:
Info:            ICESTORM_LC:   100/ 1280     7%
Info:           ICESTORM_RAM:     3/   16    18%
Info:                  SB_IO:    28/  112    25%
Info:                  SB_GB:     4/    8    50%
Info:           ICESTORM_PLL:     0/    1     0%
Info:            SB_WARMBOOT:     0/    1     0%

Look for the "ICESTORM_RAM" line. We consumed 3 RAM blocks as expected, so the synthesis tool inferred the RAM blocks correctly.

The C part is almost the same as in the previous article, the only difference is that we read few hundres/few thousands of samples from the device and print the data instead of storing it in the binary file:

int main(int argc, char *argv[]) {
    //Reading 500Mb of data from the GPIO
    const unsigned samples_count = 2500;
    uint32_t *buffer = (uint32_t*) malloc(samples_count * sizeof(uint32_t));
    poll_data_from_gpio(buffer, samples_count);

    //Calculate the ticks difference between each sample in place
    for (int i = 0; i < samples_count - 1; ++i) {
        char *ptr = (char*)(buffer + i);
        printf("%02X %02X %02X\n",
            (int)(*ptr),
            (int)(*(ptr + 1)),
            (int)((*(ptr + 2)) & 0x1F)
        );
    }

    return 0;
}

Compile and test the code:

>gcci -o3 test -o test test.c
>sudo ./test
Done !!!
FF FF 1F
FE FE 1E
FD FD 1D
FC FC 1C
FB FB 1B
FA FA 1A
F9 F9 19
F8 F8 18
F7 F7 17
F6 F6 16
F5 F5 15
F4 F4 14
F3 F3 13
F2 F2 12
F1 F1 11
F0 F0 10
EF EF 0F
EE EE 0E
ED ED 0D
EC EC 0C
EB EB 0B
EA EA 0A
E9 E9 09

The data is read correctly, hooray!

Conclusion

We learned how to use RAM in iCE40 FPGA and implemented FIFO buffer. In the next article, we will learn how to read the data from multiple I2S microphones and push it into the FIFO buffer. Stay tuned!

References

• The source code for this article is available at Github

• The Memory Usage Guide for iCE40 Devices

Introduction

GPIO could be considered one of the options for transferring data at a relatively fast speed into single-board computers (SBCs), such as the Raspberry Pi. Possible applications include capturing radio signals for software-defined radio (SDR) or processing data from a microphone array: each microphone typically captures up to 48K samples per second, and having a few tens or even hundreds of microphones can result in a significant transfer rate that needs to be managed.

SBCs, like the Raspberry Pi 4, have substantial computing power and typically a few gigabytes of RAM, in addition to exposed GPIO pins. The latter makes it easy to connect them to external devices. Thus, using them as the core of a high-speed data acquisition and processing system seems attractive.

There are two main approaches for transferring data to/from an SBC via GPIO: polling (also known as bit-banging) and using DMA. Surprisingly, both can be done in user space on RPi (although elevated privileges are needed). As shown in https://github.com/hzeller/rpi-gpio-dma-demo, polling is faster, so we will use polling in our experiments.

In ARM-based systems peripherals, such as UART, SPI, GPIO are typically memory-mapped, so we can access them by reading and writing to the physical memory addresses corresponding to the peripheral registers. In order to get access to the memory-mapped GPIO registers, we use mmap to map the /dev/mem file (which provides physical view of the memory) into the program's address space.

One of the challenges with polling, though, is that SBCs typically run Linux or another general-purpose operating system, so the CPU is a shared resource, and the system will interrupt our bit-banging process from time to time, causing the data flow to stop. Consequently, the data stream has to be buffered on the device side.

We will consider a strategy to minimize interruption of the polling process and try see what transfer rate we can acheive this way. We will also estimate the interruption time and the required buffer size on the device side which will allow not to loose any data.

Reseving a CPU core for polling. Keeping the CPU frequency at maximum

Turns out that the Linux kernel allows to "set aside" one or a few CPU cores, so the operation system won't schedule any processes to run on that cores by default. However the system is still aware of this "reserved" cores and processes can be explicitly assigned to these cores. There are a few things here we must take into account: first of all, these isolated cores are still interrupted by the system clock. We expect the interruption time to be no more than a few tenths of microseconds, but measuring it is one of the goals of this work.

The kernel command line parameter isolcpu <core> allows to "isolate set of CPU from disturbences". Let's "isolate" 3rd core of RPi4 CPU "form disturbance": here is my kernel command line params file cmdline.txt:

console=serial0,115200 console=tty1 ...[SKIPPED]... isolcpus=3

The only change I made was adding isolcpus=3 at the end of file. Now, when you boot into the system you can use a tool like top/htop and confirm that 3rd core is allways idle. It is possible to explicitly assign a process to that core:

taskset -c 3 yes > /dev/null &

Which starts a dummy process yes > /dev/null on 3rd CPU core. Our strategy is to run the polling process on the isolated core so we will have minimal interruptions from the OS.

Another important consideration is that Raspberry Pi 4 has Dynamic Voltage and Frequency Scaling (DVFS) feature, so by default the CPU core frequency is lowered when it idles. The frequence scaling policy is controlled by so-called "governors". The default governor is "ondemand", which tries to keep the CPU frequency as low as possible when the system is idle and raises it to the maximum value when the system is under load. In my experiments I found that the task assigned to the isolated core is starting to run slower and after approximatelly 60 milliseconds the speed gets 2-2.5x faster. If we want to get stable and fast cycles we need to change the CPU governor to "performance" mode for the core we want to run on. The performance governor keeps the CPU frequency at the maximum value all the time at the expense of increased power consumption and heat generation. Here is how we can do it:

sudo sh -c "echo performance > /sys/devices/system/cpu/cpu3/cpufreq/scaling_governor"

In this mode the CPU core will run at the maximum frequency all the time.

Measuring setup

To measure transfer rate and timing, we will build a simple timing device based on an FPGA, which has a fast internal counting timer. The device waits for the rising edge of the "Data Req" (data request) line and sets its 21-bit data output to the timer's value and the "Data Rdy" (data ready) line. The polling program detects the change in the "Data Rdy" line, reads and records the 21-bit data value from the parallel bus, and then sets "Data Req" to low on the SBC. This signals to the timing device that the SBC has successfully read the data, prompting it to set "Data Rdy" to low. The polling program detects the falling edge of the "Data Rdy" line and proceeds to the next cycle iteration. The difference in consecutive data reads from the timing device allows us to measure the time between loop iterations. We need to measure two values: the average number of cycles per unit of time (to determine throughput) and the maximum time between two iterations of the loop (to determine the required buffering size).

The reason we use a 21-bit data bus is that we hit the maximum number pins available on Icestick. The number of GPIO pins on the Raspberry Pi is 28, and since the protocol uses 3 lines for control, we have 25 pins remaining on the SBC side.

Here is the wiring diagram of the measuring setup:

and its real-life appearance

The exchange process described above can be visualized as follows:

The polling program (left side of the diagram) is written in C. Here is the source code of the loop:

for (int i = 0; i < size; ++i) {
    //Set the DATA_REQUEST signal to the device (25th GPIO pin)
    *(gpio_port + (GPIO_SET_OFFSET / sizeof(uint32_t))) = (1<<25);

    //Wait for the DATA_READY signal from the device (27th GPIO pin)
    while((*(gpio_port + (GPIO_LEV_OFFSET / sizeof(uint32_t))) & (1<<27)) == 0);

    //Read the data from the device, keeping only the lower 24 bits
    buffer[i] = *(gpio_port + (GPIO_LEV_OFFSET / sizeof(uint32_t))) & 0xFFFFFF;

    //Clear the DATA_REQUEST signal to the device
    *(gpio_port + (GPIO_CLR_OFFSET / sizeof(uint32_t))) = (1<<25);

    //Wait for the DATA_READY signal from the device to be cleared
    while((*(gpio_port + (GPIO_LEV_OFFSET / sizeof(uint32_t))) & (1<<27)) != 0);
}

The FPGA code is written in Verilog. Here is some highlights of the timing device design. The icestick has a 12 MHz reference clock, and we use it with PLL available on the ICE40 FPGA for generatint 50.25 MHz internal "fast" clock. So our timer resolution is approximatelly 20 ns. Here is how we declare the PLL in verilog:

wire clk; //Declare signal for 50.25MHz clock

SB_PLL40_CORE #(
    .FEEDBACK_PATH("SIMPLE"),
    .PLLOUT_SELECT("GENCLK"),
    .DIVR(4'b0000), // DIVR = 0  // 12MHz * (DIVF + 1) / (DIVR + 1) = 50.25MHz
    .DIVF(7'b1000010), // DIVF = 66
    .DIVQ(3'b100), // DIVQ = 4
    .FILTER_RANGE(3'b001) // FILTER_RANGE = 1
) pll (
    .REFERENCECLK(ref_clk), //Input 12MHz ICEStick clock
    .PLLOUTCORE(clk),       //Output 50.25MHz clock
    .LOCK(),
    .RESETB(1'b1),
    .BYPASS(1'b0)
);

The clk signal is 50.25 MHz clock, provides synchronization. The main logic of the timing device (right part of the exchagne diagram) can be described by the following verilog code:

module transfer_msr(
    input ref_clk,  //ICEStick 12MHz clock
    input rst,
    input data_req,
    output reg data_rdy,
    output reg [23:0] msr_data
);

    reg data_req_1;
    reg data_req_2;

    reg [23:0] timer_count;


    wire clk;

    //...[SKIPPED PLL declaration]...

    always @(posedge clk) begin
        if (rst) begin
            msr_data <= 24'b0;
            timer_count <= 24'b0;
            data_req_1 <= 1'b0;
            data_req_2 <= 1'b0;
        end else
        begin
            // Since the data_req comes from the external source, we need
            // to synchronize it See Harris, Harris, chapters 3.5.5, 4.4.4
            // or https://en.wikipedia.org/wiki/Incremental_encoder#Clock_synchronization
            if (data_req_1 & ~data_req_2) begin
                msr_data <= timer_count;
            end else if (data_req_1 & data_req_2) begin
                data_rdy <= 1'b1;
            end else if (~data_req_1) begin
                data_rdy <= 1'b0;
            end

            if (timer_count == 24'hFFFFFF) begin
                timer_count <= 24'b0;
            end else begin
                timer_count <= timer_count + 1;
            end

            data_req_1 <= data_req;
            data_req_2 <= data_req_1;

        end;
    end

endmodule

I use 24-bit counter because I am having I2S INMP441 microphone array as a possible follow-up project. The resolution of the INMP441 microphone is 24 bits, so I want to have the same resolution for the timer.

Results

The program reads 500M values of the timer from the FPGA and records and dumps the raw 20 lower bits of the timer to a file. I post-processed the file to calculate the time between two consecutive reads, so we can see the distribution of the time intervals.

Some observations: the typical timer increment between reads is aroun 19 timer clicks, here is the first 200 reads

23, 19, 19, 22, 19, 19, 19, 23, 20, 22, 19, 19, 19, 19, 19, 19, 19,
20, 22, 19, 19, 19, 19, 19, 19, 19, 19, 23, 19, 19, 19, 19, 20, 23,
23, 22, 20, 19, 18, 19, 19, 19, 20, 19, 22, 19, 19, 19, 20, 18, 19,
20, 18, 23, 23, 19, 19, 23, 19, 19, 19, 19, 19, 19, 19, 19, 19, 20,
19, 19, 22, 19, 20, 22, 19, 20, 18, 19, 20, 23, 19, 19, 18, 19, 19,
19, 19, 19, 20, 19, 23, 23, 22, 19, 19, 19, 19, 19, 20, 19, 22, 19,
19, 20, 19, 18, 23, 19, 20, 22, 19, 19, 19, 20, 19, 22, 19, 19, 23,
19, 19, 19, 19, 19, 23, 19, 19, 20, 19, 19, 19, 19, 19, 20, 18, 20,
23, 22, 19, 19, 19, 19, 19, 19, 20, 19, 23, 22, 19, 19, 19, 19, 19,
19, 20, 22, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 23,
22, 19, 19, 19, 19, 20, 22, 19, 19, 20, 18, 20, 22, 19, 19, 23, 19,
19, 19, 19, 20, 23, 22, 19, 19, 19, 19, 19, 19

Since the timer frequency is 50.25MHz, the typical time between reads is 19/50.25MHz = 0.378us, or approximatelly 2.6M reads per second.

Occasionaly we have a few hundreds or even a couple of thousands of timer clicks between reads, which is probably due to the the OS interrupts.

Here is the histogram which illustrates the distribution of pollng cycles timing for 500M cycles:

Overwhelming majority of the polling cycles are around 400 ns, but when we zoom out the time axis, we see two more peaks: around 5500 ns and 9500 ns

I think the peaks at 5500 ns and 9500 ns are due to the OS interrupts. Note abrupt end of the histogram at ~18000 ns.

That means if we provide the buffer for storing around 18 micoseconds of the data on the FPGA device side, we can, more or less handle the stream despite of the occasional polling delays. In microphone array application, for 100 microphones with 24-bit resolution, at 48KHz sampling rate, we need to store 100*24*48000 = 115.2M bits per second, or 14.4M bytes per second. So, for 18 microseconds delay we need to provide the buffer of approximatelly 260 bytes, which is more than feasible.

Verilog and C code is available in the github repository.

Conclusion, Takeaways, Future Work and Follow-ups

1. I really loved working with IceStick and APIO/IceStorm tools. It is a great platform for learning and prototyping. Hovewer, the number of exposed pins is very limited, and we hit the limit here

2. Synchronization of the signals coming from outside of device clock domain is super-important. I had frequent glitches without it:

3. Looks like the approach we used here allows us to connect around 50 microphones safely, and we probably need to push the speed further to connect more microphones. The bottleneck seems to be on the SBC side, I need to understand if it is possible to squeeze more speed out of the SBC. Another option would be using more powerful FPGA with big RAM attached to it and moving some of the DSP processing to the FPGA.

4. The next step would be to connect a bunch of I2S microphones to the FPGA and transfer real audio data to the SBC.

4-wire bundle

8-wire bundle

Once we figure out which wire corresponds to which winding we can come up with a wiring scheme: we will feed the stator winding with two signals having \(90^\circ\) phase shift between them, so the winding will generate rotating magnetic field inside the resolver. The rotor winding will generate sinusoidal voltage which will have phase shift relative to the stator's voltage. The phase shift will correspond to the shaft angle \(\phi\).

We will use left and right audio channels of the sound card to generate two \(90^\circ\) shifted reference signals. We will use two channels of the LINE IN: one channel will be used to read the reference signal and another channel will be used to read the output signal from one of the rotating winding. So will use the following wiring scheme:

Having both reference and output signals helps us to compensate for the unkown phase shift introduced by the sound card circuitry.

Here is video of the test run of the setup:

In order to measure the shaft angle we convolve the output signal from rotor with the reference signals:

Using

and

we can obtain the following relationships between \(A, B\) and \(\phi\):

Since we are creating a software implementation, we operate in discrete time domain, so we use the discrete counterparts of the formulas above:

This computation is peformed for both reference and output signals, so we get reference angled \(\phi_{ref}\) and output angle \(\phi_{out}\). The shaft angle is then \(\phi = \phi_{out} - \phi_{ref}\).

It is easier if each period corresponds to exact number of samples, so we adjust the frequency slightly: we will use 400.909Hz instead of 400Hz. This way we will have 110 samples per period at 44100 samples per second. \(N\) is the number of samples in the signal, must be exact multiple of period.

The source code available on GitHub:.

Here is the video of the final test run: